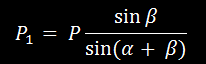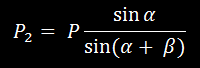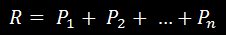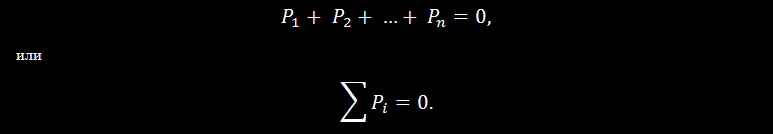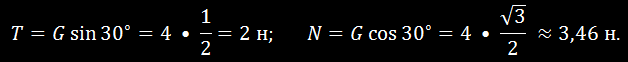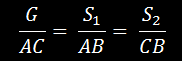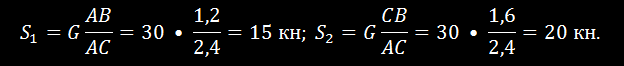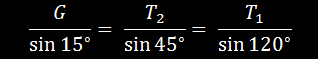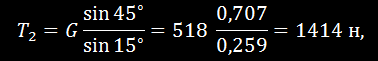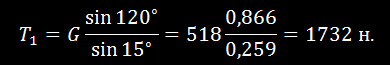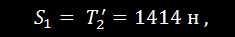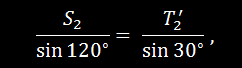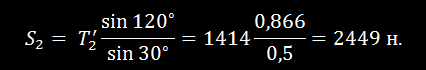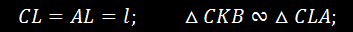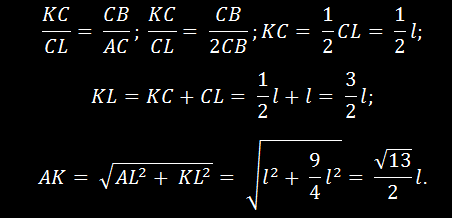18:59 22.09.2012
XXI
Механика является одной из древнейших наук, которая своим возникновением и развитием обязана потребностям практики.
Энгельс отмечает, что развитие механики тесно связано с развитием земледелия (подниманием воды для орошения в Египте), с ростом городов, возведением крупных построек, развитием ремесла и мореплавания. Известно, например, что при постройке египетских пирамид применялись некоторые простейшие механические приспособления: рычаги, блоки, наклонная плоскость. Таким образом, еще в древние времена человечество обладало некоторыми эмпирическими знаниями по механике, но потребовался длительный период времени для того, чтобы установить основные законы механики и заложить фундамент этой науки.
В древности не существовало деления науки по отраслям знаний, а поэтому механика, наряду с философией, естествознанием и другими естественными науками, являлась составной частью единой науки о природе и обществе.
Лишь после Аристотеля (384—322 гг. до н. э.) начинается процесс выделения отдельных частных наук из общего естествознания.
На первой стадии развития механики, от древнего мира до эпохи Возрождения (14—16 вв.), в результате изучения простейших машин создается учение о силах.
Основоположником механики как науки является знаменитый ученый древности Архимед (287—212 гг. до н. э.) Архимед дал точное решение задачи о равновесии сил, приложенных к рычагу, и создал учение о центре тяжести тел. Кроме этого, Архимед открыл и сформулировал закон о гидростатическом давлении жидкости на погруженное в нее тело, который носит его имя.
Быстрое и успешное развитие механики начинается лишь с эпохи Возрождения, когда создаются условия для развития науки и техники.
В эпоху Возрождения, как отмечает Энгельс, «... были заложены основы для позднейшей мировой торговли и для перехода ремесла в мануфактуру, которая, в свою очередь, послужила исходным пунктом для современной крупной промышленности. Духовная диктатура церкви была сломлена».
«Это был величайший прогрессивный переворот из всех пережитых до того времени человечеством, эпоха, которая нуждалась в титанах и которая породила титанов по силе мысли, страсти и характеру, по многосторонности и учености»
*.
С эпохи Возрождения начинается следующий период развития механики. Для решения практических задач требуются исследования движений тел. На основе накопленного за четыре столетия опыта к концу XVIIв. создаются основы динамики — науки об общих законах движения материальных тел.
Блестящим представителем эпохи Возрождения является знаменитый итальянский художник, физик, механик и инженер—Леонардо да Винчи (1451—1519). На основании своих исследований в области механики Леонардо да Винчи установил, что сила трения скольжения не зависит от величины поверхности соприкасания трущихся тел. Кроме того, Леонардо да Винчи занимался изучением движения падающего тела, движения тела по наклонной плоскости и ввел в механику понятие момента силы.
Зарождение небесной механики — науки о движении небесных тел — связано с великим открытием Николая Коперника (1473—1543) — созданием гелиоцентрической системы мира, сменившей геоцентрическую систему Птоломея.
Это открытие произвело переворот в научном миросозерцании той эпохи — освободило естествознание от теологии. На основании учения Коперника и астрономических наблюдений Кеплер (1571—1630) сформулировал три закона движения планет, которые впоследствии привели к открытию Ньютоном закона всемирного тяготения.
Создание основ динамики принадлежит великим ученым — итальянцу Галилео Галилею (1564-1642) и англичанину Исааку Ньютону (1643—1727).
В своем знаменитом сочинении «Математические начала натураль¬ной философии», изданном в 1867 г., Ньютон в систематическом виде изложил основные законы так называемой классической механики. Эти законы, установленные на основании наблюдений и опытов Ньютона и его предшественников, являются объективными законами природы.
XVIIIв. характеризовался разработкой общих принципов классической механики и важнейшими исследованиями по механике твердого тела, гидродинамике и небесной механике.
Наиболее крупными зарубежными учеными XVIIIи XIXвв. в области механики являются Иван Бернулли (1667—1748), Даниил Бернулли (1700—1782), Даламбер (1717—1783), Лагранж (1736—1813), Шаль .(1793—1880). В работах французских ученых Вариньона (1654—1722) и Пуасо (1777—1851) наряду с динамикой дальнейшее развитие получила и статика. Вариньон решил задачи сложении сил, приложенных к одной точке, и параллельных сил; он установил условия равновесии этих сил и доказал теорему о моменте равнодействующей. Вариньону принадлежит создание основ графостатики (построение силового и веревочного многоугольников).
* Ф. Энгельс. Диалектика природы. Госполитиздат, 1950, стр. 4.
Развитие науки в России связано с образованием по инициативе Петра I в 1725 г. в Петербурге Российской Академии наук. Большое влияние на развитие механики оказали труды гениального русского ученого, основателя Московского университета, акад. М. В. Ломоносова (1711 — 1765) и знаменитого математика, астронома и физика Леонарда Эйлера (1707—1783).
За 130 лет работы в Российской Академии наук Эйлер создал большое количество работ по математике, механике твердого и упругого тела, гидромеханике и небесной механике.
Огромное значение для дальнейшего развития механики имеют работы выдающихся отечественных ученых XIX и XXвв.: М. В. Остроградского (1801 — 1861), П. Л. Чебышева (1821—1894), С. В. Ковалевской (1850—1891), А. М. Ляпунова (1857—1918), И. В. Мещерского (1859—1935), К. Э. Циолковского (1857—1935), А. Н. Крылова (1863—1945), Н. Е. Жуковского (1847—1921), С. А. Чаплыгина (1869—1942) и ряда других ученых.
Деятельность русских ученых, несмотря на крайне тяжелые условия развития науки в дореволюционной России, значительно способствовала развитию как общей теоретической механики, так и специальных механических дисциплин.
Великая Октябрьская социалистическая революция создала исключительно благоприятные условия для развития науки в нашей стране. Благодаря этому советские ученые в области механики освоили богатое наследие русской дореволюционной науки и своими работами обогатили сокровищницу мировой науки.
В многочисленных научно-исследовательских институтах и вузах Советского Союза в настоящее время ведется большая работа по дальнейшему развитию механики.
Тесная связь науки и практики в СССР обеспечивает прогресс механики, при помощи которой решаются многочисленные задачи, выдвигаемые практикой социалистического строительства.
РАЗДЕЛ ПЕРВЫЙ
Теоретическая механика — это наука, в которой изучаются общие законы механического движения и механического взаимодействия материальных тел.
Механическим движением называется перемещение тела по отношению к другому телу, происходящее в пространстве и во времени.
Курс теоретической механики делится на три раздела: статику, кинематику и динамику.
Статикой называется раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу.
Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
Динамикой называется раздел механики, в котором изучается движение материальных тел в пространстве в зависимости от действующих на них сил.
Приступая к изучению статики, следует определить основные понятия механики, встречающиеся в этом разделе.
Материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать, называют материальной точкой. Материальная точка обладает массой и способностью взаимодействовать с другими телами. Например, при изучениии движения планет солнечной системы вокруг Солнца их размерами по сравнению с их расстояниями от Солнца пренебрегают и рассматривают эти планеты как материальные точки.
Системой материальных точек, или механической системой, называется такая совокупность материальных точек, в которой положение и движение каждой точки зависят от положения и вижения других точек этой системы.
В теоретической механике рассматриваются такие тела, расстояния между любыми точками которых остаются неизменными. Такие тела называются абсолютно твердыми телами.
Полагая тела абсолютно твердыми, не учитывают деформаций, которые возникают в реальных телах. Это значительно упрощает изучение действия сил на тело и условий, при которых эти силы уравновешиваются.
Условия равновесия сил, приложенных к абсолютно твердому телу, используются при изучении действия сил на деформируемое тело.
Твердое тело может находиться в состоянии покоя или некоторого движения. Каждое из этих состояний условимся называть кинема¬тическим состоянием тела.
Важнейшим понятием теоретической механики является понятие силы. Взаимодействие двух тел, способное изменить их кинематиче¬ское состояние, называется механическим взаимодействием.
Сила — это мера механического взаимодействия тел, определяю¬щая интенсивность и направление этого взаимодействия.
Сила определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Сила изобра¬жается вектором (рис. 1). Прямая, по которой направлена данная сила,
называется линией действия силы. За единицу силы в Международной системе единиц измерения СИ (в механике система МКС) принимается ньютон (н). Совокупность нескольких сил, действующих на данное тело или систему тел, называется системой сил.
Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называются экви-валентными.
Сила, эквивалентная некоторой системе сил, называется равно-действующей.
Система сил, которая, будучи приложена к твердому телу, нахо-дящемуся в покое, не выводит его из этого состояния, называется системой взаимно уравновешивающихся сил.
Силы, действующие на механическую систему, делят на две группы: внешние и внутренние силы.
Внешними называют силы, действующие на материальные точки '. (тела) данной системы со стороны материальных точек (тел), не принадлежащих этой системе.
Внутренними называют силы взаимодействия между материаль¬ными точками рассматриваемой системы.
Основной задачей статики является исследование условий равновесия внешних сил, приложенных к абсолютно твердому телу.
Приступая к изучению курса статики твердого тела, рассмотрим аксиомы, лежащие в основе этого курса. Эти аксиомы сформулиро¬ваны на основе наблюдений и изучения окружающих нас явлений реального мира. Некоторые основные законы механики Галилея — Ньютона являются одновременно и аксиомами статики.
Под действием взаимно уравновешивающихся сил материальная точка (тело) или находится в состоянии покоя, или движется прямолинейно и равномерно.
Аксиома инерции выражает установленный Галилеем закон инерции.
Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны (Рис. 2).
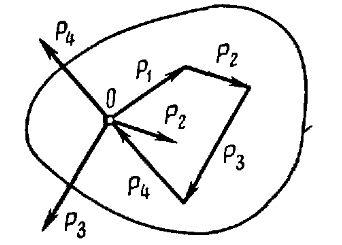
Если к твердому телу, находящемуся под действием некоторой системы сил, приложить уравновешивающуюся систему или исключить такую систему сил, то получится система сил, эквивалентная заданной системе.
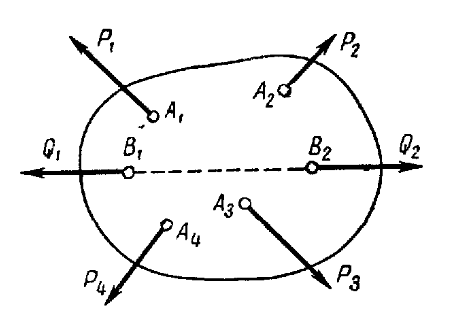
Пусть, например, к твердому телу приложены силы P1, P2, P3 и P4, под действием которых тело находится в покое или совершает какое-то движение (рис. 3). Приложим к телу две равные противоположно направленные силы Q1 и Q2, которые взаимно уравновешиваются.
Если тело в покое, то оно сохранит его; если тело в движении, то оно будет двигаться под действием новой системы сил Q1, Q2, P1, P2, P3 и P4 так же, как под действием сил P1, P2, P3 и P4, т. е. новая система сил эквивалентна прежней.
Это же произойдет, если из заданной системы сил, приложенных к твердому телу, исключить взаимно уравновешивающиеся силы, входящие в ее состав.
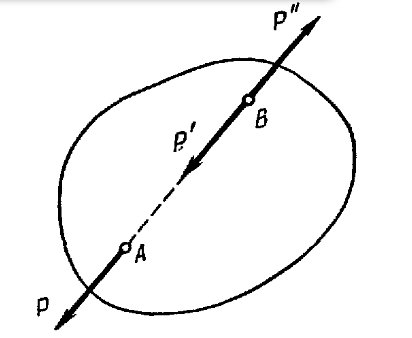
Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменными ее модуль и направление.
Предположим, что к твердому телу в точке А приложена сила P (рис. 4). Приложим в точке B две силы Р' и Р",
равные по модулю силе P и направленные по ее линии действия в противоположные
стороны. Затем отбросим силы P и Р"
как взаимно уравновешивающиеся. Тогда к телу в точке B будет приложена
сила Р' = P,
эквивалентная силе Р в точке A.
Таким образом, силу можно переносить в любую точку по линии действия, не изменяя ее
модуля и направления. Поэтому в статике твердого тела сила рассматривается как скользящий вектор.
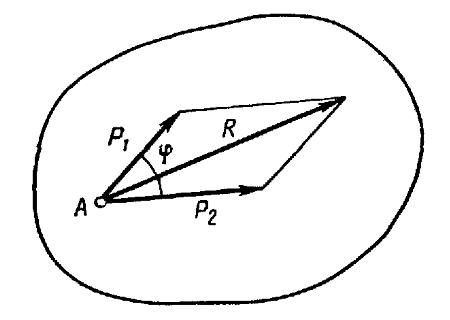
Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается
диагональю параллелограмма, построенного на этих силах (рис. 5).
Это положение, хорошо известное из элементарного курса физики, выражается следующим геометрическим равенством:
R = P1 + P2
Модуль равнодействующей силы определяется по следующей формуле:
Всякому действию соответствует равное и противоположно направленное противодействие.
Эта аксиома утверждает, что силы действия друг на друга двух тел равны по модулю и направлены по одной прямой в противоположные стороны. Таким образом, в природе не существует одностороннего действия силы.
Аксиома действия и противодействия установлена Ньютоном и известна как один из основных законов классической механики.
Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердевании.
Из этой аксиомы следует, что условия равновесия сил, приложенных к абсолютно
твердому телу, должны выполняться и для сил, приложенных к деформирующемуся телу. Однако в
случае деформирующегося тела эти условия необходимы, но недостаточны. Так, например, условие
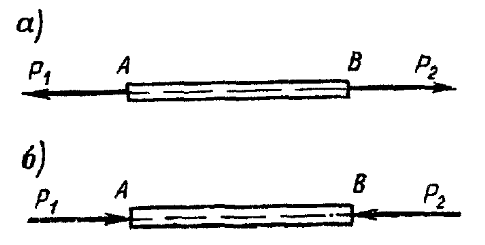
равновесия двух сил, приложенных к твердому стержню на его концах, состоит в том, что силы
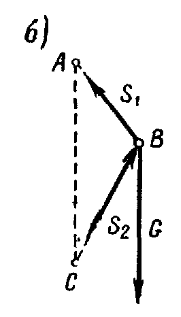
равны по модулю и направлены по одной прямой в противоположные стороны (рис. 6,а и б).
Две уравновешивающиеся силы, приложенные к нити, удовлетворяют этому условию, но при наличии добавочного условия — силы должны только растягивать, а не сжимать нить (рис. 6,а).
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью.
Твердое тело, свобода движения которого ограничена связями, называется несвободным.
Все силы, действующие на несвободное твердое тело, наряду с делением на внешние и внутренние силы, можно также разделить на задаваемые силы и реакции связей.
Задаваемые силы выражают действие на твердое тело других тел, вызывающих или способных вызвать изменение его кинематиче¬ского состояния.
Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело.
Одним из основных положений механики является принцип освобождаемости твердых тел от связей, согласно которому несвободное твердое тело можно рассматривать как свободное, на которое, кроме задаваемых сил, действуют реакции связей.
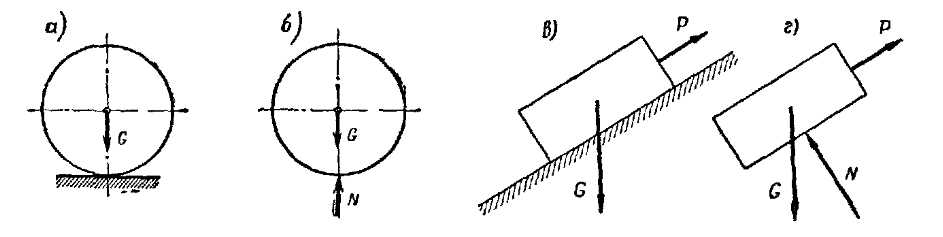
Пусть, например, на гладкой неподвижной горизонтальной плоскости покоится шар (рис. 7, а).
Плоскость, ограничивая движение шара, является для него связью. Если мысленно освободить шар
от связи (рис. 7, б), то для удержания его в покое к нему в точке касания с плоскостью нужно
приложить силу N, равную весу шара G
по модулю и противоположную ему по направлению. Сила N и будет
реакцией плоскости. Тогда шар, освобожденный от связи, будет свободным телом, на которое
действует заданная сила G и реакция плоскости N.
Гладкая плоскость не противодействует перемещению тела вдоль плоскости под действием задаваемых
сил (рис. 7, б), но не допускает его перемещения в направлении, перпендикулярном к плоскости.
Поэтому действие плоскости на тело выражается нормальной реакцией N (рис. 7, г).
Реакция гладкой плоскости направлена перпендикулярно к плоскости.
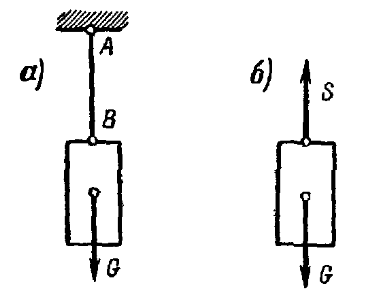
Если к концу B нити AB, прикрепленной
в точке A, подвесить груз весом G (рис. 8, а),
то реакция S нити будет приложена к грузу в точке B,
равна по модулю его весу G и направлена вертикально вверх (рис. 8, б).
Реакция нити направлена вдоль нити.
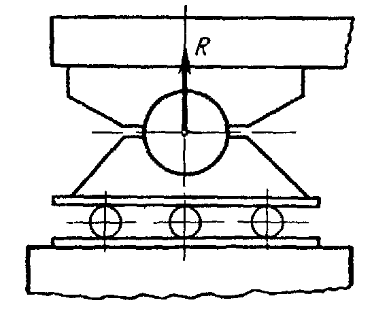
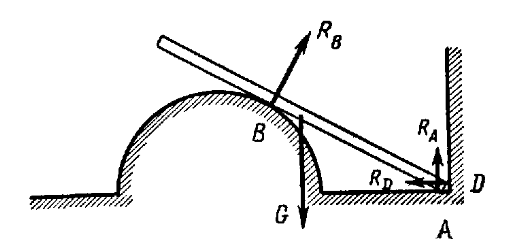
Пусть балка весом G в точке B
опирается на гладкую поверхность, а в точках A и D — на
гладкие горизонтальную и вертикальную плоскости (рис. 9). Тогда реакции опорной поверхности и
опорных плоскостей будут иметь указанные на рис. 9 направления.
Определение модулей этих реакций показано после установления условий равновесия сил, произвольно расположенных на плоскости (
§ 25).
Для определения каждой реакции нужно знать три ее элемента: модуль, направление и
точку приложения. Точка npиложения реакции, как правило, бывает известна. Направление же реакций известно лишь для некоторых типов связей. Если существуют два взаимно перпендикулярных направления на плоскости, в одном из которых связь препятствует перемещению тела, а в другом нет, то направление ее реакции противоположно первому направлению.
Так, например, гладкая горизонтальная плоскость препятствует перемещению шара вертикально вниз и не препятствует его горизонтальному перемещению. В этом случае реакция плоскости направлена вверх (рис. 7, б). Так же определяется направление реакции нити (рис. 8).
Гладкая поверхность, на которую опирается балка точкой B (рис. 9),
препятствует перемещению балки по нормали к поверхности вниз и не препятствует перемещению
вдоль оси балки. Поэтому реакция этой поверхности направлена по нормали к поверхности вверх.
Аналогично, если балка опи¬рается на ребро в точке D (точечная
опора), то реакция в точке D направлена перпендикулярно к оси балки
(рис. 10).
Рассмотрим два основных типа опор балок и их реакции.
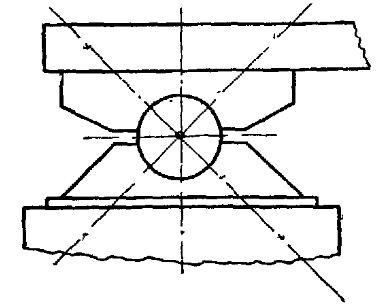
На рис. 11 изображена шарнирно-неподвижная опора, которая препятствует любому поступательному
движению балки, но дает ей возможность свободно поворачиваться вокруг оси шарнира. По своей
конструкции такая шарнирная опора состоит из двух обойм, из которых одна закреплена на балке,
а другая — на неподвижной поверхности. Эти обоймы соединяются при помощи цилиндрического
валика (на рис. 11 показано среднее сечение конструкции). В зависимости от действующих сил,
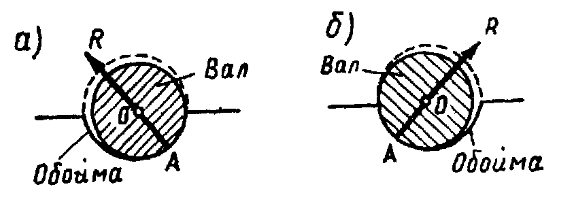
валик может прижиматься к различным точкам обоймы. Реакция R такой
опоры проходит через центр шарнира O и точку соприкасания A
(рис. 12а, б). Линия действия реакции этой опоры всегда проходит через центр шарнира, но
модуль и направление реакции не известны.
Шарнирно-подвижная опора, нижняя обойма которой поставлена на катки, не препятствует перемещению балки параллельно опорной плоскости (рис. 13). Если не учитывать трения катков, то линию действия реакции такой опоры следует считать проходящей через центр шарнира перпендикулярно к опорной плоскости.
Таким образом, не известен лишь мо-дуль этой реакции.
В курсе теоретической механики обычно рассматривают только действие внешних сил
на абсолютно твердое тело. Однако при расчете различных конструкций бывает необходимо определять
внутренние силы, возникающие в растянутых и сжатых стержнях. Для определения внутренних усилий
в стержнях воспользуемся так называемым методом сечения, дающим возможность переводить интересующие
нас внутренние силы в разряд внешних сил. Рассмотрим сущность этого метода.

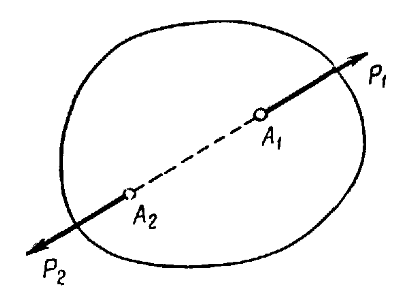
Пусть стержень AB, весом которого пренебрегаем, растягивается
двумя равными по модулю силами P1 и P2,
приложенными к его концам (рис. 14). Рассечем мысленно стержень, разделив его на две
произвольные части AD и DB. На часть
AD действуют две уравновешивающиеся силы: внешняя сила P1
и внутреннее усилие S1, заменяющее
действие отброшенной части стержня. Из второй аксиомы следует, что внутреннее усилие S1
направлено по оси стержня и равно по модулю силе P1.
Внутреннее усилие S1, выражающее
действие отброшенной части DB на рассматриваемую AD,
является по отношению к рассматриваемой части стержня внешней силой.
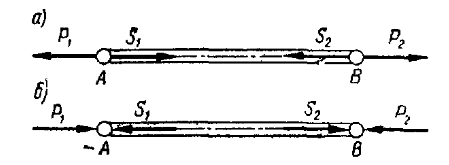
Если стержень AB растягивается (рис. 15, а) или сжимается
(рис. 15, б) силами P1 и
P2, то на тела, вызывающие
его растяжение или сжатие, со стороны стержня действуют реакции S1 и S2.
При этом реакции растянутого стержня равны по модулю задаваемым силам и направлены
по оси стержня от его концов.
Реакции сжатого стержня равны по модулю заданным силам и направлены по оси стержня
к его концам. Так как реакции и внутренние усилия по модулю равны, то для определения усилия
в стержне достаточно определить его реакцию.
Сходящимися называются силы, линии действия которых пересекаются в одной точке.
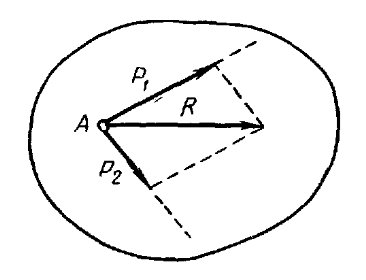
Если к телу приложены две силы, линии действия которых пересекаются в одной точке,
то, как указывалось в аксиоме параллелограмма сил, их равнодействующая приложена в точке A
пересечения линий действия сил; она изображается диагональю параллелограмма, построенного на
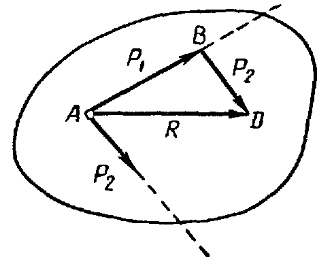
этих силах (рис. 16). Построение параллелограмма сил можно заменить построением треугольника
сил ABD (рис. 17). Направление равнодействующей силы R
по контуру силового треугольника противоположно направлению обхода контура треугольника, определяемому
слагаемыми силами.
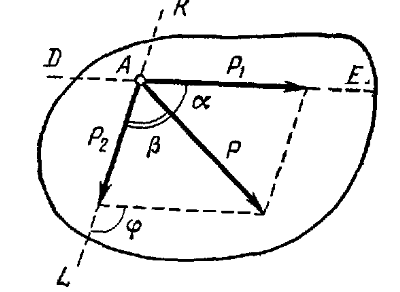
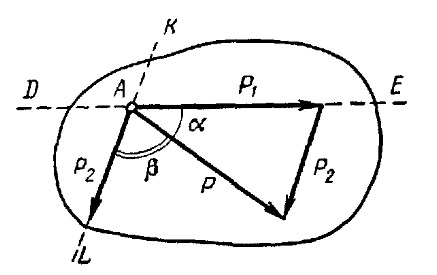
При помощи параллелограмма или треугольника сил можно решить и обратную задачу — разложить
силу P на две составляющие P1
и P2, приложенные в той же
точке и направленные по заданным линиям действия KL и DE
(рис. 18 и 19).
Используя известные формулы тригонометрии (теорему синусов), имеем
Так как
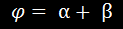
, то
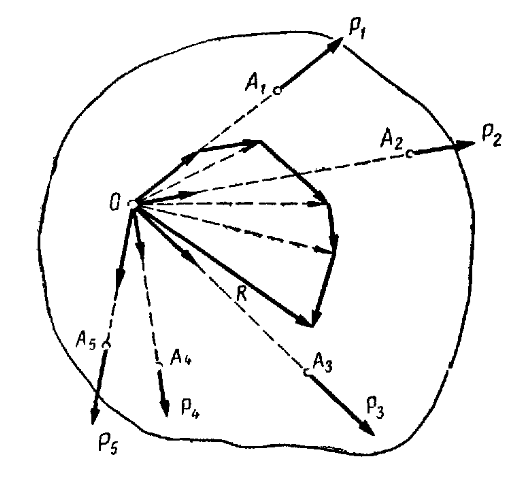
Пусть к твердому телу в точках A1,
A2, A3,
A4 и A5
приложены сходящиеся силы P1,
P2, P3,
P4 и P5
(рис. 20). Все эти силы можно перенести в точку O пересечения их
линий действия и, строя треугольники сил, последовательно сложить. Тогда равнодействующая этих
сил изобразится замыкающей стороной многоугольника сил. Таким образом, равнодействующая R
сходящихся сил приложена в точке пересечения линий действия сил и равна их геометрической сумме:
Следует учитывать то, что направление равнодействующей по контуру силового многоугольника
противоположно направлению обхода контура этого многоугольника, определяемому направлением первой силы.
Сходящиеся силы уравновешиваются в том случае, если их равнодействующая равна нулю, т. е. многоугольник сил замкнут (рис. 21):
В замкнутом многоугольнике сил все силы направлены по контуру многоугольника в одну
сторону.
Частный случай.Три сходящиеся силы уравновешиваются, если треугольник этих сил замкнут.
Все задачи на равновесие сил, приложенных к некоторому телу (точке) решаем по следующему плану:
- Показываем действующие на тело задаваемые силы.
- Мысленно освобождаем тело от связей, заменяя их действие соответствующими силами - реакциями связей.
- К полученной системе сил применяем условия равновесия, со-ответствующие этой системе.
- Определяем искомые величины.
Пример 1. На гладкой наклонной плоскости AB, образующей
с горизонтом угол a = 30°, при помощи веревки DE,
параллельной плоскости AB, удерживается однородный шар весом
G - 4 н. Определить давление шара на плоскость и натяжение веревки
(рис. 22,а).
Решение.Решаем задачу по изложенному плану, рассматривая равновесие сил, приложенных к шару.
- Показываем действующую на шар, задаваемую силу - вес шара G,
приложенный в центре шара (рис. 22,6).
- Мысленно освобождаем шар от связей, заменяя действие связей их реакциями. Связями
для шара являются наклонная плоскость AB, реакция
которой приложена в точке соприкасания K и направлена
перпендикулярно к плоскости, и веревка DE, реакция
которой направлена вдоль веревки.
- К шару приложены три сходящиеся силы: вес шара G, реакция
N плоскости AB и реакция
T веревки DE. К этой системе
сил применяем условие равновесия трех сходящихся сил, т. е. строим замкнутый
треугольник этих сил. Для этого откладываем заданную силу Q
(рис. 22,s). Из конца b силы G
следует провести прямую, параллельную линии действия либо реакции T,
либо реакции N. Проведем из конца b
силы G прямую, параллельную реакции T,
тогда из начала а силы G должна быть проведена прямая,
параллельная другой реакции N (рис. 22,в). Точка пересечения
c проведенных прямых является третьей вершиной треугольника
сил. Стороны треугольника должны иметь такое направление, чтобы все силы G,
T и N были направлены
в одну сторону по обходу контура треугольника.
- Из треугольника сил, определив его углы, находим модули искомых реакций:
- Из треугольника сил, определив его углы, находим модули искомых реакций:
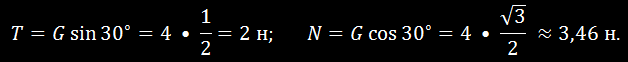
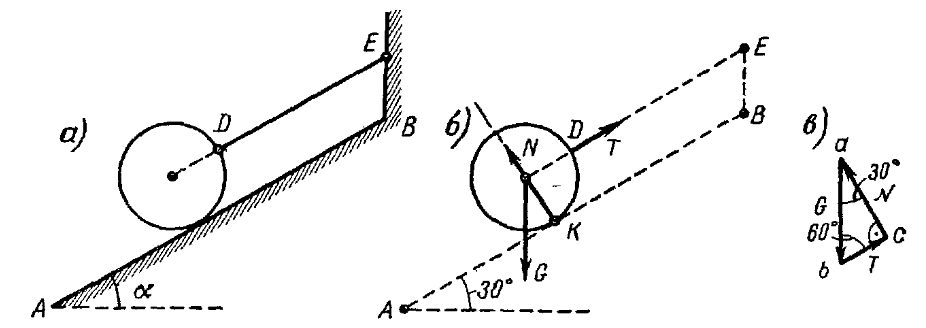
Рис. 22
Найденные реакции T и N
прикладываем к шару (рис. 22,(б). Давление шара на плоскость и сила, растягивающая веревку,
по модулям равны найденным реакциям, направлены противоположно им и приложены в точках D
и K к плоскости и к веревке (на рисунке эти силы не указаны).
Примечание.Условие равновесия всегда применяется к системе сил, действующей на одно тело. Поэтому
всегда определяются не давления тела на опоры, а реакции опор, которые вместе с задаваемыми
силами действуют на рассматриваемое тело.
В примере 1 условие равновесия применялось к силам, действующим на шар, а потому определялись
приложенные к шару реакции опор, а не давления шара на опоры.
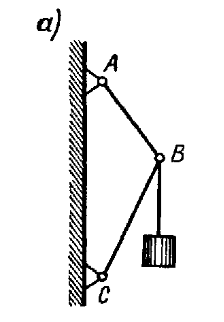
Пример 2. Кран состоит из цепи AB = 1,2 м и подкоса CB = 1,6 м,
прикрепленных к вертикальной стойке в точках A и C,
причем AC = 2,4 м. В точке B подвешен
груз весом G = 30 кн. Определить усилия S1 в цепи и
S2 в подкосе (рис. 23,а).
Рис. 23
Решение. Решаем задачу по общему плану, не выделяя его отдельных пунктов. Рассматриваем
равновесие трех сил, приложенных к узлу B: заданной силы G
и реакций цепи и подкоса S1
и S2, линии действия которых
совпадают с отрезками AB и CB (рис. 23,б).
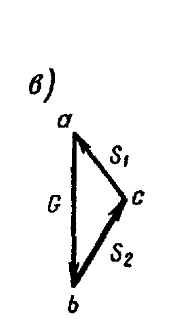
Строим замкнутый треугольник abc этих сил (рис. 23,в). По треугольнику
сил определяем направления реакций S1
и S2. Приложив найденные реакции
к узлу В (рис. 23,б), устанавливаем, что растянута только цепь, а подкос сжат. Так как стороны
треугольника сил и треугольника ABC соответственно параллельны, то
эти треугольники подобны. Из подобия следует:
Из этих равенств определяем искомые усилия:
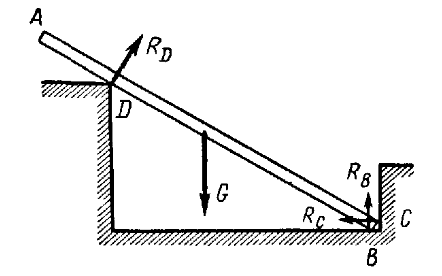
Пример 3. Груз весом G = 518 н подвешен в точке D
к канату ADE, участок которого ADCоставляет
с горизонталью угол 30°, а участок DE угол 45°. В точке A
канат привязан к вертикальному столбу AB, поддерживаемому подкосом
AC, наклоненным к горизонтали под углом 60°. Определить натяжение
каната на участках AD и DE и усилия в
столбе и подкосе (рис. 24а).
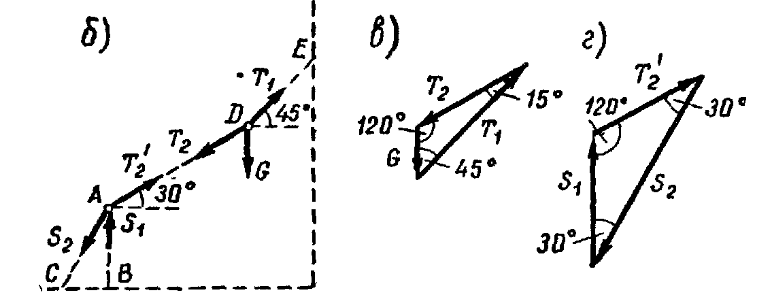
Решение. В этой задаче следует рассматривать отдельно равновесие сил, приложенных
к каждому из узлов D и A. На узел D
действуют заданная сила G и реакции T1
и T2 частей каната DE
и AD, а на узел A — реакция T1'
каната AD, а также реакции столба и подкоса S1
и S2(рис. 24,6). Прикладываем
к узлу D заданную силу G и строим замкнутый
треугольник сил G, T1
и T2, действующих на этот
узел (рис. 24,в). Определив углы треугольника сил, по теореме синусов находим:
откуда
Рис. 24б, в, г.
Затем строим треугольник сил T1',
S1, S2.
приложенных к узлу A, откладывая прежде всего реакцию
T1'
каната AD, которая по модулю равна реакции T2,
приложенной к узлу D, а по направлению противоположна ей (рис. 24,г). Из равнобедренного треугольника сил находим:
откуда
Приложив все найденные силы к узлам D и A
(рис. 24,6), устанавливаем, что столб AB сжат, а подкос AC растянут.
Линии действия трех непараллельных, взаимно уравно¬вешивающихся сил пересекаются в одной точке.
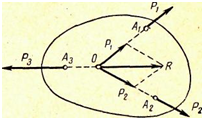
Пусть к твердому телу в точках A1, A2 и A3
приложены три непараллельные взаимно уравновешивающиеся силы P1, P2, P3
(рис. 25). Так как силы P1 и P2
расположены в одной плоскости, то эти силы можно перенести в точку O
пересечения их линий действия и определить их равнодействующую R,
которая будет приложена в этой же точке. Так Рис. 25. как по условию силы P1,
P2 и P3
уравновешиваются, то силы P3
и R должны быть равны по модулю и направлены по одной прямой в противоположные
стороны. Следовательно, линия действия силы P3
проходит через точку O, что и требовалось доказать.
Рис. 25
Примечание.Если две заданные силы P1,
и P2 параллельны, то, как
известно из элементарного курса физики, линия действия уравновешивающей силы P3
параллельна линиям действия заданных сил и находится от линий действия этих сил на расстояниях,
обратно пропорциональных модулям сил.
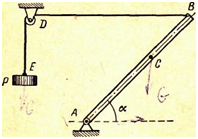
Пример 4. Рама AB весом G = 1,5 кн
может вращаться вокруг оси шарнира A. Центр тяжести рамы C
определяется по условию AC = 2CB. Рама
удерживается под углом a = 45° к горизонтали веревкой BDE,
к концу E которой подвешен груз P. Участок
BD горизонтален. Определить вес груза P
и реакцию шарнира A при равновесии сил, пренебрегая трением на блоке
(рис. 26, а).
Рис. 26
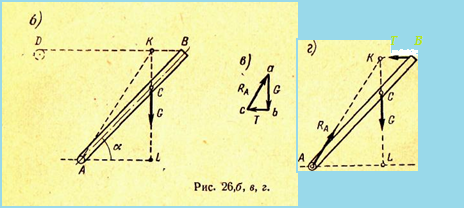
Решение. Решаем задачу по изложенному выше плану, рассматривая равновесие сил, приложенных
к раме AB (рис. 26, 6").
Рис. 26bcd
1. Показываем действующую на раму заданную силу — вес рамы G,
прикладывая его в центре тяжести C
2. Мысленно освобождаем раму AB от связей, заменяя
их действие соответствующими реакциями. Реакция веревки T приложена
в точке B и направлена по прямой BD,
реакция шарнира RA приложена
в точке A, но линия действия ее не известна.
3. К системе трех уравновешивающихся сил G, T,
RA, приложенных к раме, применяем
теорему о равновесии трех непараллельных сил.
Линии действия сил G, T, RA
должны пересекаться в одной точке. Находим точку K пересечения линий
действия сил G и T; через эту же точку
должна пройти линия действия реакции RA;
определяем эту линию, соединяя точки A и K.
Строим замкнутый треугольник трех сил, сходящихся в точке K (рис. 26,в).
4. Определяем искомые величины, т. е. реакции T и RA
следующим образом. На рис. 26,б строим треугольник ALK, стороны
которого соответственно параллельны сторонам треугольника сил. Определяем стороны треугольника
ALK.
Обозначаем AL = l. Так как a = 45°, то
Отсюда имеем
Треугольник сил abc подобен треугольнику AKL. Стороны треугольников пропорциональны.
Применим метод приведения силы к заданному центру к сложения сил, произвольно расположенных на плоскости
Нестреляй, Нестреляй, Нестреляй, Нестреляй...IOI
Эй начальник
Еду я на Родину
Государственных шлюх
И не дай им опять закатать рукава
Неплачь напрасно
Пусть года бегут напрасно
Ей Эй ЕЭЕй ЭЭЭЭЭЭЭЭЭй ЕЕЕЕЕй ЭЭЭЭЭЭЭЭЭЭЭййййййййй Эй
Мудрецов полно, а путь один
От глупых теорем оставленных в пыли
бЮДЖЕТ ПРОСТО БЕШЕННЫЙ
<<наша КРЫШЫ НЕБА ГОЛУБАЯ>>
вОСЕМЬ, это вместе со мной было
сОРВАННЫМ ЛИСТОМ КРУЖИТЬ
Подруги говорят
Он просто
припев
Если, Если уууууууу доживу
Если, Если aaaaaaaa доживу
aaaaaaaaaaaaaaaaaaaaaaaaaa
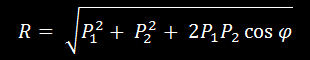



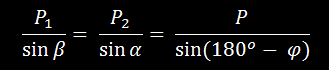
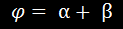 , то
, то