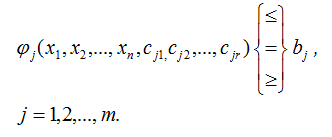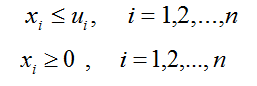Тема1. Классификация задач принятия решений (2 часа)

Условия существования задач принятия решений (ЗПР). Классификация ЗПР: прямые и обратные ЗПР; детерминированные ЗПР, стохастические ЗПР и ЗПР в условиях неопределенности; однокритериальные и многокритериальные ЗПР.

Тема 2. Постановка ЗПР (2 часа)

Вербальная и формальная постановка задач принятия решений. Построение математической модели ЗПР

Тема 3. Детерминированные ЗПР. Задачи линейного программирования (ЛП). ( 6 часов)

Графический метод решения задачи. Построение искомой области решений. Нахождение оптимального решения. Алгебраический метод решения задач линейного программирования. Симплекс метод решения задач ЛП.

Тема 4. Детерминированные ЗПР. Транспортная задача. ( 6 часов)

Определение транспортной задачи и область ее применения. Решение транспортной задачи. Методы нахождения начального решения: правило северо-западного угла, метод наименьшей стоимости и приближенный метод Фогеля. Метод потенциалов для поиска оптимального решения. Задача о назначениях.

Тема 5. Динамическое программирование в ЗПР ( 4 часов)

Примеры задач динамического программирования. Задача распределения капиталовложений. Математическая модель задачи динамического программирования. Рекуррентные соотношения и алгоритмы обратной и прямой прогонки.

Тема 6. Сетевые модели в ЗПР. (4 часа)

Примеры сетевых задач. Типы сетевых задач: минимизация сети, нахождение кратчайшего маршрута, определение максимального потока. Методы решения сетевых задач.

Задачи принятия решений

1. Принятие решений - это специфический, жизненно важный процесс человеческой деятельности , направленный на выбор наилучшего варианта действий .

2. Задачи принятия решений (ЗПР) условно можно подразделить на 2 больших вида:

Ежедневно встречающиеся и решаемые на основе опыта и здравого смысла, с незначимыми последствиями. Примеры.

Сложные задачи, для принятия решения по которым необходимы расчеты. Пример: организация городского транспорта. Необходимо принять решения: какое количество и каких транспортных средств направить по тому или иному маршруту? Какое количество остановок нужно и где их нужно размещать?

Примеры сложных задач

Участники процесса принятия решений

лицо, принимающее решение;

эксперты;

консультанты

Теория принятия решений – область исследования, вовлекающая понятия и методы математики, статистики, экономики, менеджмента и психологии; изучает закономерности выбора людьми путей решения разного рода задач, а также исследует способы поиска наиболее выгодных из возможных решений

Задачей принятия решений назовём пару , где X – множество вариантов, ОП – принцип оптимальности, дающий представление о качестве вариантов, в простейшем случае правило предпочтения вариантов;

Решением задачи является множество Xоп E X, полученное с помощью принципа оптимальности ОП.

Когда для обоснования и принятия решений применяются те или иные математические методы, то мы имеем дело с исследованием операций.

Операцией называется всякая система действий (мероприятие), направленная на достижение определенной цели.

Операция является управляемым мероприятием. Всякий определенный выбор зависящих от нас параметров называется решением.

Оптимальным называются решения, по тем или иным показателям предпочтительные перед другими. Цель исследования операций - количественное обоснование принимаемых решений.

Прямые ЗПР отвечают на вопрос: что будет, если в заданных условиях мы примем какое-то решение х Е Х ?

Обратные ЗПР как выбрать решение х, чтобы показатель эффективности W обратился в максимум (минимум) ?

В зависимости от вида показателя эффективности (критерия оптимальности) различают следующие ЗПР:

- ЗПР в условиях определенности (детерминированные ЗПР). Детерминированные ЗПР характеризуются наличием принципа оптимальности, позволяющим поставить каждому варианту из множества R вполне определенный исход.

- ЗПР в условиях риска (стохастические ЗПР). В стохастических ЗПР зависимости между вариантами и их исходами носят вероятностный характер.

- ЗПР в условиях неопределенности. ЗПР в условиях неопределенности характеризуются отсутствием (в силу не исследованности) зависимости между вариантами и их исходами.

По количеству целей ЗПР подразделяются на:

Однокритериальные (задачи с одной целевой функцией);

Многокритериальные (задачи с несколькими признаками предпочтения)

Постановка задач принятия решений

Наличие исходного множества вариантов, равнозначных с точки зрения достижения поставленной цели;

Наличие критерия оптимальности;

Наличие системы ограничений, накладываемых на возможные способы достижения цели.

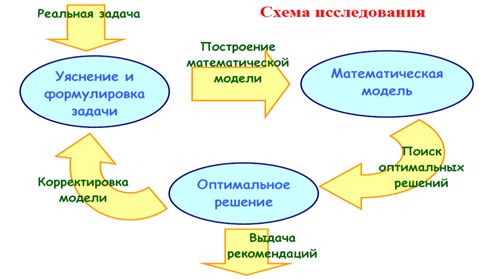
Этапы процесса принятия решения:

Вербальная постановка задачи принятия решения

Формализация исходной проблемы

Построение математической модели

Поиск оптимального решения (решение модели)

Проверка адекватности модели

Реализация решения

На всех этапах, предшествующих получению оптимального решения математической модели, успех зависит от опыта и творчества всей команды (специалистов-аналитиков и заказчиков задачи принятия решений), занимающейся решением задачи исследования операций

Вербальная постановка задачи принятия решения

формулируется цель (конструктором, технологом);

Качественная цель характеризуется тем, что всякий возможный исход (решение) либо обеспечивает достижение этой цели, либо не обеспечивает.

Количественная цель характеризуется стремлением обеспечить получение той или иной технико-экономической характеристики проектируемого объекта

определяются способы и средства достижения цели;

ресурсы, которые необходимы для достижения цели;

состав технико-экономических показателей, необходимых для адекватной оценки альтернативных вариантов достижения цели.

Формализация исходной проблемы

описание возможных альтернативных решений

выбор варьируемых параметров

определение критерия оптимальности и задание целевой функции

построение системы ограничений

Построение математической модели

перевод формализованной задачи на язык математических соотношений

попытка построить математическую модель как одну из стандартных математических моделей

если модель очень сложная и не приводится к стандартному типу, ее следует упростить, либо применить эвристический подход, либо методы имитационного моделирования

Поиск оптимального решения (решение модели)

Применение известных методов оптимизации, методов имитационного моделирования или эвристических подходов

Исследование чувствительности оптимального решения к отклонению варьируемых параметров

Проверка адекватности модели

Оценка полученного решения: имеет ли оно смысл и приемлемо ли интуитивно

Сравнение полученного решения с известными ранее моделями или поведением реальной системы

Реализация решения

Перевод результатов решения модели в рекомендации, комплекты технической документации или другие документы, понятные для лиц принимающих решение – заказчиков решения исходной проблемы

Математическая модель – объективная схематизация основных аспектов решаемой задачи или ее описание в математических терминах. Включает в себя множество изменяемых переменных, целевую функцию и ограничения, записанные в виде математических соотношений или заданные соответствующими вычислительными алгоритмами.

Составление матмодели объекта очень ответственная задача, требующая глубоких знаний не только или не столько в математике, столько в существе моделируемых явлений.

Предназначение и роль математических моделей

Возможность применения строгих, точных и универсальных математических методов;

Возможность использования статистических, экспертных, нормативных данных и новых информационных и вычислительных технологий;

Исключение необходимости проведения дорогостоящих экспериментов на исследуемом объекте;

Возможность многократного экспериментирования на модели без дополнительных капиталовложений;

Получение наилучших вариантов решения проблемы (исходной задачи).

Изменяемые переменные – переменные, оптимальные значения которых должны быть найдены в ходе решения математической модели задачи исследования операций:

Целевая функция – функция, вычисляющая количественное выражение критерия оптимальности:

Эта функция достигает экстремума, когда ее аргументы принимают значения, описывающие оптимальное решение задачи в соответствии с заданным критерием. Эта функция зависит как от изменяемых переменных x1,x2,…,xn, так и от параметров задачи a1,a2,…,al, которые принимают фиксированные значения, определяемые ее условием.

Ограничения

– неравенства или равенства, определяющие область допустимых значений (ОДЗ) изменяемых переменных, в которой осуществляется поиск решения (экстремума целевой функции).Часто выделяют два специфических типа ограничений:

простые ограничения сверху:

Рассмотрим почти «школьную» задачу построения оптимального решения: найти длину a, ширину b и высоту c прямоугольного параллелепипеда, имеющего наибольший объем V при заданной площади поверхности S.

Математическая модель задачи:

Варьируемые параметры – a, b, c. Необходимо найти максимум целевой функции F(a,b,c)=V(a,b,c)=abc; max F(a,b,c);

при ограничениях в виде равенства и неравенств:

2ab+2ac+2bc=S; a > 0; b > 0; c > 0;

Модифицируем задачу: требуется найти длину a, ширину b и высоту c прямоугольного параллелепипеда, имеющего заданный объем V при заданной площади S.

Математическая модель задачи:

Варьируемые параметры – a, b, c.